The major scale is the most commonly used scale in Western Music. That’s how awesome it is. We want to use it all the time. In the western world, babies come out of the womb singing the major scale. It’s really well ingrained into our cultural landscape.

Before we look at the major scale, let’s first look at the general concept of a scale. A scale is simply a series of notes. Any series of notes is a scale. We can make one up right now, and if it’s not already in common use, we could even name it after ourselves and we’d have our own scale.

Let’s make up a scale right now, just as an example. Here’s my scale:

C D# E F# G A# B C

We’re going to call that the C Classick scale. As far as I know, that is not a series of notes that is in common use, so essentially I just invented it just now.

If I play a song using only those notes, I’m in the key of C Classick. So, let’s make some general distinctions:

1. A scale is a series of notes. If you play all those notes in a row, you are playing that scale.

2. If you are using some or all of the notes from that scale in various different configurations, you are in that particular KEY.

Example:

Here’s a C major scale:

C D E F G A B C

If I play the following notes on a piano, all of which are from the above scale

G B C D F E A C

I am in the key of C. I have not played a C major scale but I have used the notes from the C major scale.

So, let’s start by looking at the major scale specifically. The major scale is built on a pattern of half steps and whole steps. The pattern is this:

Whole step, whole step, half step, whole step, whole step, whole step, half step

If I start from ANY note and follow that pattern, I will have built myself a major scale. Let’s use C as our starting note and build a major scale.

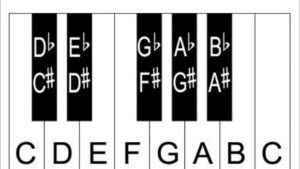
In the previous post, we looked at using a slightly different method for constructing the major scale. This was to start from the first note and add the note that is a major 2nd up, a major 3rd up, a perfect 4th up, and so on. Review this post if necessary. You will see that, whatever method we employ, we end up with the same notes.

Method One – The pattern of whole steps and half steps just described. (W-W-H-W-W-W-H)

Method Two – Start from any note and add the note that is a major 2nd up, a major 3rd up, a perfect 4th up, a perfect 5th up, and major 6th up, and a major 7th up.

To re-iterate, if you start from any note and follow the pattern W W H W W W H, you will end up with a major scale. The distance from the first note to the second note will be a Whole Step/Major Second, The distance from the first note to the third note will be 2 Whole Steps/Major Third. The distance from the first note to the fourth note will be 2 1/2 Whole Steps/Perfect Fourth. The distance from the first note to the fifth note will be 3 1/2 Whole Steps/Perfect Fifth. The distance from the first note to the sixth note will be 4 1/2 Whole Steps/Major Sixth. The distance from the first note to the seventh note will be 5 1/2 Whole Steps/Major Seventh. The distance from the first note to the 8th note will be 6 Whole Steps/Octave.

If we play the notes above (the notes in the C major scale) all the way up, we have just played a C major scale. If we use the notes from that scale and mix them up to make up melodies, we are in the key of C.

Except When We're Not!

There is another concept that we’ll get to a bit later called “modes.” This is when you use all of the notes of a major scale, but place strong emphasis on a particular note, so that that note becomes the tonal center. For example, we can use all of the notes from the C major scale, but place strong emphasis on the note D, and we’ll be playing in a “mode” of the C major scale called “D Dorian.” Don’t worry about this right now, but I just wanted to mention it as a caveat to the information that was just presented about “always being in the key of C” when we are using all of the notes from the C major scale. More later.

Now, let’s do the same thing, except starting from G.

We use the same pattern of whole steps and half steps to build this scale. All of the intervals from the first note to the other notes are the same as in the C major scale we built. As a matter of fact, ALL of the intervals between all of the notes are exactly the same. This scale is identical to the C major scale in every way, except that we started from a different note, and therefore all of the notes in the scale are different. It would be like using a template to build a house, but putting them in different cities, or painting them all different colors. All the measurements would be exactly the same, but they would be…well, in different cities or painted different colors.

In fact, the G major scale and the C major scale SOUND identical EXCEPT for the fact that they start on different notes. So, if we were to play a C major scale, and then go up (or down) to G and play a G major scale, the only difference would be that one would be higher or lower.

Let’s use a song that we all know to use as an example. Let’s say you’re at a party and you start singing Happy Birthday, but quickly everyone realizes that it is much to high for them. Someone says, “That’s too high, can we sing it lower?” What they mean is that they want to sing it in a lower key. The melody (Happy Birthday to you, Happy Birthday to you….) is the same melody. It’s the same melody because the distance between all of the notes is exactly the same. When you lower is (or raise it) so it fits better in your vocal range, you are just choosing to change the key by using the notes from a different major scale. It may be that you starting using the notes from the C major scale (Happy Birthday, by the way, is comprised solely from notes in the major scale,) but that was too high, so you dropped the whole thing a minor third to A so you could sing it a little more easily. You changed the key.

The C major scale and the G major scale and every other major scale are just like the song Happy Birthday in this sense. They sound the same because the distance between all of the notes is exactly, precisely the same. The only difference is that each major scale STARTS on a different note.

You may be asking yourself, “If all of the major scales sound exactly the same, why do we have so many of them? Why don’t we just have one and make it easier?”

We answered one of those question already. Sometimes things just don’t work for vocalists or certain instruments in a certain key, and if we change the key, they sit much better. But, the more important reason, which we’ll examine in much more detail later, is the fact that lots of music changes key during the course of the music. Most pop and folk music tends to stay in one or two keys, but classical music and jazz may change keys quite a bit more. It’s not uncommon for a jazz tune to change keys every couple seconds. (That’s one of the reasons jazz can be a little more challenging to listen to, by the way.)

The Concept of Tonal Center

The C major scale has seven different notes. (C, D, E, F, G, A, and B.) Why then, do we call it the C major scale? What is it about C that makes it more important than all of the other notes? Who does this C think she is?

There are actually a lot of reasons, and we’d ultimately have to consult a book on the physics of music to get a comprehensive answer to this question. (If you’re interested, Leonard Bernstein covers this topic on a series of lectures he gave at Harvard which are available on DVD.) However, we aren’t going to go into all of the science behind what it is that gives C (in the case of the C major scale) special importance. (If we were talking about the G major scale, it would be G that had special importance.) All we really need to know is that when when we play a C major scale, or we are playing in the key of C, for whatever reason, the note C feels most like home. It feels like a resting place. The song doesn’t really feel resolved and complete until someone plays the note C. (If we sing Happy Birthday in the key of C, the final note is C.) Everything in the C major seems to just point back to C. The note C makes everything feel resolved. That word resolved (or more often, the word resolution) is a very, very important word in music. If you’d like a more in-depth exploration of the concept, go here.

So far, we know a few important things about the major scale:

So far, we’ve constructed two major scales: C and G. Let’s look at them again:

C D E F G A B C

G A B C D E F# G

Pretty awesome, aren’t they? We’ve taken two of the notes that exist in Western music and built major scales off of them. We can do this for all twelve pitches that we use in Western music, and we will, whether you like it or not. But let’s consider a couple of things first. Like this particular issue:

While there are only twelve pitches in Western music

(and even this isn’t really true, because we bend and slide and use “pitches between the pitches” all the time)

there are more than twelve NOTES. Oh god nooooooo!!!!

Remember the chromatic scale that we looked at when we started? Many of the notes have more than one name. (Like C#/Db.) C# and Db are the same pitch. They sound EXACTLY the same. But C# and Db are different notes.

Another way to say this is: C# and Db are found on the exact same point on any instrument, but:

1. When we write them on staff paper they appear as different notes.
2. When we discuss them, we refer to them by different names. (C# or Db.)

To re-cap this confusing concept: C# and Db are the same pitch, but they are different notes. There is a word for this, which we discussed briefly in the first section of this blog (Name of Notes and Intervals.) The name for this weird concept is: Enharmonic. C# is enharmonic to Db.

Why is this discussion of enharmonicism important to this lesson on the major scale? Because, at this point, we want to learn every major scale, and if we don’t understand the concept of enharmonic notes, we will trip over one detail. The detail is this: There are twelve different pitches, but there are fifteen major scales. Three of the pitches produce major scales that have enharmonic equivalents. (Huh? What does that sentence mean?)

This is what I mean. Here are all of the major scales:

1. C
2. C# (Enharmonic Equivalent to Db)
3. Db (Enharmonic Equivalent to C#)
4. D
5. Eb
6. E
7. F
8. F# (Enharmonic Equivalent to Gb)
9. Gb (Enharmonic Equivalent to F#)
10. G
11. Ab
12. A
13. Bb
14. B (Enharmonic Equivalent to Cb)
15. Cb (Enharmonic Equivalent to B)

So, as it turns out, while there are only twelve different pitches, there are actually fifteen different major scales. The scales that are enharmonic to each other (like C# and Db) sound exactly the same. We just call them by different names, and we write them out differently.

Let’s compare two of these major scales to verify their enharmonicsim. We’ll look at C# and Db.

C# D# E# F# G# A# B# C#

Db Eb F Gb Ab Bb C Db

Looking at these two scales leads us to the last of two concepts we need to cover in order to have a full understanding of this.

1. Why to Use Enharmonic Spellings: Let’s look at the piano again, and find each pitch in each of the above scales. In each case, each pitch is in exactly the same place on the piano. The pitch C# and the pitch Db are in exactly the same place (where there are two black keys grouped together, C#/Db is the left of the two.) Going to the next note, you’ll notice that D# and Eb are both found in the exact same place on the keyboard.

Now let’s move on to the weird one. What is UP with E# and F? If we look at the piano, there really doesn’t seem to BE an E#. We can find E pretty easily, and right next to it is F. So, where’s E#? There’s no black key after E, which we would think would be E#, but there’s not. There’s only F. The only logical answer is that E# is F. E# and F are the same note.

Ugh. Music theory sucks. When do I get to learn how to play “Sweet Home Alabama?”

But, there is an actual logical reason for this. Let’s look back at our C# major scale again. The scale proceeds in a nice, neat, alphabetical way: C#, D#, E#, F#, G#, A#, B#, and back to C#. (“But E# is F! Why can’t I just call it F???) Ok, calm down. Here’s why. Let’s write the scale out again, but this time we’ll call E#: “F.” Which it is. Even though it’s….not.:

C# D# F F# G#……

See the problem? We end up with two F’s. Can you imagine writing out music, and every time you came to an F, you had to tell the musician whether it was F natural or F sharp? What a pain. It’s a pain to do, and it’s a pain to read. For everyone’s convenience, it’s actually easier to call the note in question E#. That way the scale has every alphabetical note represented, and none of them are repeated.

You’ll notice that the same thing happens in this scale for the note B#. We could just call it C (Which it is. Even though it’s not.) But if we did this, we’d have two C’s. Can you really imagine if the scale looked like this:

C# D# F F# G# A# C C#

as opposed to this:

C# D# E# F# G# A# B# C#

The latter is much easier to read, talk about, and think about. Believe me, if you are reading music off of the page, the version without two kinds of “C’s” and two kinds of “F’s” is much easier to deal with.

2. Why We Don’t (Commonly) Use Some Enharmonic Equivalents: There is one other little issue that may or may not have occurred to you. If it hasn’t occurred yet, it would have at some point, so I’m going to head it off at the pass. Think about this for a moment: The note A# is enharmonic to Bb. There is a Bb major scale. Why then, is there no A# major scale? We could ask the same question about D#. D# is enharmonic to Eb. There’s an Eb major scale, but there is no D# major scale. We could even ask the same question about F and E#. There is an F major scale…but there is no E# major scale.

The in each of these cases is that there is. There is an E# major scale. There is an A# major scale. There is a D# major scale. It’s just that they are so cumbersome to use, that we really don’t use them. We tend strongly towards their enharmonic equivalents. Why is this?

Let’s spell out an A# major scale, remembering the following rule: Each alphabetical letter must be represented once, and cannot be repeated. (Meaning, we can’t have, say, a D-natural and a D-sharp.)

The scale would proceed like this:

Whole step up to

C – ?

Uh-oh.

You may have to take a second to orient yourself by looking at a keyboard in order to figure this one out. Start at A#. Go up a whole step to what we’re calling B#. You’ll notice that that is “C” on our keyboard. (B# is enharmonic to C.) If we go a whole step up from there we arrive at what on our keyboard looks like “D.” But in this context we can’t call it “D.” In this context we call it “C double-sharp.” (We signify a double-sharp with an “X”.) Ugh. Sad, but true. In order to follow the “rules” (using every alphabetical letter in order without skipping or repeating notes) the only way we can spell this scale is: A# B# Cx D# E# F# GX A#.

So, as you can see, there are some major scales we avoid, because using them is so cumbersome. You don’t really need to know why. I just wanted to make sure that, while you were sitting up at night thinking with reverence about the concepts of music theory that you’ve learned in this blog, that when you finally got around to thinking, “Hey….how comes there’s a Bb major scale, but there’s no A# major scale? After all, A# is the enharmonic equivalent of Bb. What’s up with that?” You can soothe your aching mind by reminding yourself that is has “something to do with all that double sharp stuff.”

One last thing on that subject. We do use double sharps and flats in music sometimes. It’s not really common, but it’s not exactly uncommon either. They definitely show up.

Let’s review what we have learned in this treatment of the major scale. We’ll start by repeating the four main things that we already mentioned, and then we’ll add a few:

1. The major scale is the most commonly used scale in western music.
2. A major scale is constructed using a pattern of whole steps and half steps (W-W-H-W-W-W-H)
3. If we use the notes of a particular major scale (C major, for example) to create melodies, those melodies will be in that key (the key of C major, for example.)
4. Each major scale has seven different notes in it, but its name is based on the most important note (the first note of the scale,) which has special importance, because it creates a particular type of resolution. It feels like home. It is the tonal center. In the key of C, the note C is the tonal center. C feels like home.
5. Two notes are enharmonic to each other when they refer to the same pitch. Db and C# are enharmonic to each other. They are the same pitch. They sound the same. They are found at the same place on any instrument. They are the same pitch, but they are different notes. They are enharmonic to each other.
5. There are 15 major scales in common use. We could use more than these, but they require us to use double sharps and double flats, so we avoid them.

Now that we’ve learned a lot of general information about the major scale, in our next post, we’re going to dig in and just start building and learning major scales. This is going to be the practical stuff you’ve been waiting for!