
Names of Notes & Intervals
Welcome to music theory 101. We’re going to teach you everything you need to know about music theory, starting from the very beginning.
The most basic thing you can learn is the names of the notes. While this seems pretty simple, there are a couple of curve balls, namely the fact that every note actually has two names, and you have to figure out which name to use in a particular situation.
The next thing we’re going to learn is what to call the distance between two notes. (i.e. how far is it from C to F?) The distance between two notes is called the interval between those notes. (i.e. the interval from C to F is a perfect fourth.)
This is the foundation of all of our work in the music theory department: learning the nomenclature.
This first part is a little dry, but stick with it. It has real value.
Here is a piano, with the names of the notes written on the keys. I want you to know the names of the notes, and the distance between them. We call the distance between two notes an interval. This lesson is concerned with the names of notes, and the names of the intervals between them. This is going to be REALLY exciting. Believe me.
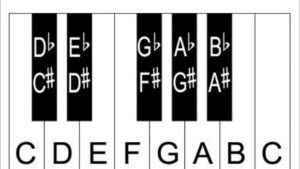
The Names of Notes
Before we get started, let me give you some tools that will allow you to drill the concepts we are talking about.
This one lets you practice identifying notes on the staff (you can change it to bass clef.)
And this one helps you work on the names of intervals.
There are other great tools on that site, and I highly advise using them.
And here is a chart with the names of all the intervals. You may not understand this now, but you should when you read this lesson and the next one.

There are only twelve notes. Imagine. All that music, and only twelve notes. Here they are, in all their majesty:
C C#/Db D D#/Eb E F F#/Gb G G#/Ab A A#/Bb B
The # symbol stands for “sharp.” The b symbol stands for “flat.” Therefore, the names of the notes are:
C
C sharp/D flat
D
D sharp/E flat
E
F
F sharp/G flat
G
G sharp/A flat
A
A sharp/B flat
B
So, what’s up with those notes that have two names? Like C#/Db. Do we ever call a note C#/Db? No. That would be totally silly. It’s an either/or deal. Sometimes, based on the context, we call it C#. Sometimes, we call it Db. You’ll understand why later. But, for now, just know that some notes have two names. They are easy to identify on the piano, because they’re black. On other instruments, it’s not as easy to tell which ones they are.
When a note has two names, that is called “Enharmonic.” I’ll use it in a sentence: C# is enharmonic to Db.
Why this two name thing? It’s a long story, but just think of them as notes that swing both ways. Sometimes that black key wants to think of itself as being a half-step above C, and we call it C# (C sharp.) Sometimes, it wants to think of itself as being a half-step below D, and we call it Db (D-flat.) Got it? The black note between the white notes C and D is sometimes called C#, and other times it’s called Db.
The rest of the names of the notes, the white keys, as it were, are pretty easy. I don’t really think they need much explaining.
Names of Intervals
The distance between two notes is the referred to as the interval between two notes. Let’s start with the most basic one: the half-step, also called a minor second.
We’re going to get back to this, so remember it!
Two notes that are right next to each other are a half-step apart. C and C# are a half step apart. C# and D are a half step apart. Now move up to E. Here’s one people get hung up on: E and F are a half-step apart. Yes. It’s true. Yeah, they’re both white. Yeah, they’re both natural notes (no sharps or flats.) But they are also RIGHT NEXT TO EACH OTHER!!! They are a half-step apart. Notes that are right next to each other, be they black or white, are a half-step apart. The smallest interval in western music is a half-step. All of the notes below are a half-step apart:
C C#/Db D D#/Eb E F F#/Gb G G#/Ab A A#/Bb B
Now, that interval of a half step has another name. It’s called a minor second. Let’s analyze that choice of a name, and see if we approve. Why do we call it a “second?”
The name “second” (or third, or fourth) is derived from how the names of the notes relate to each other ALPHABETICALLY. (You should keep in mind that the musical alphabet ends at G and then starts over.) If “A” is the first, then “B” is the second and “C” is the third. But, “A” isn’t always the first. (That would be too easy.) “C” might be the first. In that case “D” is the second, and “E” is the third.
How far is it from D up to E? D is 1 (our starting point.) That would mean that E is 2. It is a second up. From D to E is a second. E is a second up from D. The distance between D and E is a second. How far is it from G up to A.?
G is our starting point. G is 1. That would mean that A is 2.
A is a second up from G.
That’s a second. They are divided by the interval of a second. They are the first and second alphabetical letters in a series.
Now, let’s try this, just for fun. How far is it from G up to B?
It’s a third.
How far is it from F to C?
It’s a fifth.
Here’s what it comes down to: COUNT THE LETTERS.
Let’s go back to the concept we were initially investigating: Why do we call a 1/2 step a ‘minor second?”
Let’s look at a concrete example:
Db is a 1/2 step up from C.
Let’s analyze this relationship alphabetically, ignoring the flats and sharps part of it:
1 2
C D
So, it’s clear from the above example that we are dealing with some kind of second. But what kind of second?
Here’s the answer. Are you ready?
From C to Db, which is a 1/2 step, is a MINOR SECOND. From C to D, which is a WHOLE step, is a MAJOR SECOND.
Now, let’s quickly look at one of the little tricky areas that comes up all the time in music theory. We won’t dwell on it, but it’s useful to know: The interval between C and Db is a 1/2 step, or a minor second. Db and C# are the same note, just called by a different name. The interval between C and C# is a 1/2 step.
But you cannot call it a minor second. Why? The alphabetic logic conundrum! You might call it an “Augmented First” or something obtuse like that. But, it CAN’T be a second, because if “C” is ONE, then C# is…..like, still some kind of one. Again, don’t make yourself too crazy with this, but it goes like this: The distance from C to Db is a 1/2 step, and we call this internal a minor second. The distance from C to C# is a half step, but we cannot call this interval a minor second, because alphabetically speaking, if C is 1, then C# is also, uh….1. We in music theory land know this makes you crazy, but if you think dwell on it for a few minutes you’ll see that even though you don’t like it, it makes sense. Trust us. It does.
Two half steps put together are a WHOLE STEP.
C C#/Db D D#/Eb E F F#/Gb G G#/Ab A A#/Bb B
Start at C. Go a half step up to Db. Then go another half step up to D. You’ve just gone a whole step. C to D is a whole step. Now, from D, go a half step up to Eb. Now, go another half step up to E. You’ve just gone up a whole step. D to E is a whole step. From E, go a half step up to F. Now go another half step up to F#. E to F# is a whole step. This one gets people. Don’t let it get you. Now, starting on F#, go a half step up to G. Now, go another half step up to G#. F# to G# is a whole step.
A whole step is called a MAJOR SECOND.
The oversimplified point that I am trying to make, is that
A HALF STEP IS CALLED A MINOR SECOND.
A WHOLE STEP IS CALLED A MAJOR SECOND.
You can go a major second up, or a major second down. We always went up in the examples I gave you, but you can go down if you want to. Here are 7 intervals I want you to memorize for now. Just memorize them. Don’t think about them too much:
1 whole step = Major Second
2 whole steps = Major Third
2 1/2 whole steps = Perfect Fourth
3 1/2 steps = Perfect Fifth
4 1/2 steps = Major Sixth
5 1/2 steps = Major 7th
6 whole steps = Octave
Look at the piano for a second to examine this:

This is the crux of this lesson, and without much more explanation, I just want you to commit this to memory. Don’t worry about why some are called major, and some are called perfect. Don’t worry about anything else you don’t understand yet. Just memorize:
A major second up from C is D. From C to D is a major second.
A major third up from C is E. From C to E is a major third.
A perfect fourth up from C is F. From C to F is a perfect fourth.
A perfect fifth up from C is G. From C to G is a perfect fifth.
A major sixth up from C is A. From C to A is a major sixth.
A major seventh up from C is B. From C to B is a major seventh.
An octave up from C is C. From C to the next highest C is an octave.
